This last week, the first thing that was taken care of was finishing the x/y/z spin basis representation. Having fixed the Wigner small d-function in the Rotation class, the tests for this were put into the pull request and the pull was merged into the sympy master, making this my first pull request since starting GSoC. There is still some changes that will come for the Rotation class, namely the creation of a symbolic WignerD class which is returned by the current Rotation.D and Rotation.d functions, but that will be dealt with in a later pull request.
With the x/y/z basis stuff finally out of the way, I moved back to getting the Glebsch-Gordan coefficient/Wigner-3j symbols to a state where they can be pulled. Having fallen behind in getting the CG coefficient simplification to a suitable state and with the work on the x/y/z spin basis pushing the timeline back even further, the current goal is to merge what I have so far and move on to the coupled spin states. What I have so far is the classes for the Wigner-3j symbols and the Clebsch-Gordan coefficients which can be manipulated symbolically and evaluated, and a very rough version of the cg_simp method. Currently, this method can handle 3 numerical simplification, however the code is still messy and having more cases would be ideal. That said, in an effort to make sure the key parts of this GSoC project are covered, I'll be moving into writing the coupled spin states.
For the spin states portion of this project, I will develop a means of writing coupled and uncoupled spin states. The uncoupled product basis states will be written using the TensorProduct, which is in the current quantum module; each of the states in the tensor product will be states as they are currently implemented. To represent coupled basis spin states, the current spin states will be modified to included a coupled parameter. This value stores the J_i's of the spin spaces which are being coupled. In addition to the spin states being implemented, methods will be written to utilize the CG coefficients mentioned earlier to go between coupled and uncoupled basis representation. Look for more next week as this code is fleshed out.
Saturday, June 25, 2011
Saturday, June 18, 2011
More CG simplification and wrapping up x/y/z spin bases
For the first part of this last week, I continued on my work to get sums of Clebsch-Gordan coefficients to simplify. Using the same general logic that I outlined in the last blog entry, besides general cleaning up of the code, most of the work at the beginning of the week was spent on trying to develop a function that could check an expression for CG coefficients matching a set of conditions.
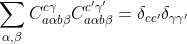
While the current method would be able to check for specific values on the CG coefficients, I have yet to come up with a good way to check that the m1 and m2 values are the same when they can take any value, as in this example. As it stands, this code still seems like quite a hack and will need some work before it is good to go.
What is left with this part of the project is:
- Getting simplification to work with sums of products of terms (as in the example above)
- Applying CG symmetries to perform simplifications
- Simplification of symbolic CG sums
- Fixing up the printing of CG terms
- Final testing/documentation
This part of the project has unfortunately fallen behind the preliminary schedule by a bit, as it was due to be finished up last week. I'll outline what I'm currently working on finish up next, but hopefully I can finish the CG stuff ASAP so I can move on to working on the spin stuff which is the true meat of the project and try to get back on schedule.
The rationale behind trying to write such a method is that it would make it much easier to identify the times where symmetries could be utilized. With such a method, the process of checking for CG coefficients could be done in a single function and the logic for implementing CG symmetries could be handled in this one function. The current method uses lists of tuples to specify the conditions on CG coefficients. For example, if the j1 value of a CG coefficient needed to be =0, you could pass the tuple ("j1",0), or if the m1 and m3 values match ("m1","m3"). All the conditions for each CG coefficient are combined into a single tuple. The current snag with simplifications of sums of products of CG coefficients. For example:
While the current method would be able to check for specific values on the CG coefficients, I have yet to come up with a good way to check that the m1 and m2 values are the same when they can take any value, as in this example. As it stands, this code still seems like quite a hack and will need some work before it is good to go.
What is left with this part of the project is:
- Getting simplification to work with sums of products of terms (as in the example above)
- Applying CG symmetries to perform simplifications
- Simplification of symbolic CG sums
- Fixing up the printing of CG terms
- Final testing/documentation
This part of the project has unfortunately fallen behind the preliminary schedule by a bit, as it was due to be finished up last week. I'll outline what I'm currently working on finish up next, but hopefully I can finish the CG stuff ASAP so I can move on to working on the spin stuff which is the true meat of the project and try to get back on schedule.
After meeting with my project mentor, Ondrej, on Wednesday, it was decided that the focus would shift to finishing up the work I'd started on x/y/z spin bases and representation of spin states that I'd started before GSoC had officially started.
The first order of business was identifying an error in the Wigner small-d function, which is used extensively in the changing of spin bases. With Ondrej noting that the small-d function was defined only on a small interval and then me discovering the bug in the Rotation.d method, we were able to address this. However, no sooner had this been done than Ondrej is able to work out a better equation for the small-d function, which will likely replace the current implementation.
Other than this, most of the work this week on the x/y/z basis representation was in documentation, testing and generally cleaning up the code to be pulled. The current pull request (my first work to be submitted since the start of GSoC) is still open here. While this pull integrates the current work on basis representation, after this pull there is still some work that will need to be done testing both the Wigner small-d and the D functions, for both symbolic and numerical values, and ensuring they return the correct results. Because the representation code relies so heavily on these functions, it is imperative that these functions evaluate properly. Once these are fully tested, there will also likely need to be more tests to ensure all the representation code returns the right values for as many odd cases as would be necessary to test. Hopefully I can finish this up soon and move on to other work that still needs to be done.
Saturday, June 11, 2011
More improvements to the simplification method
I was out of town for the beginning of this week, so I don't have as much to report, nevertheless in the last few days, I have made some good improvements to the cg_simp method, allowing it to simplify cases other than just the simple sums, tho it still only handles the same case as before involving the sum of . While it is entirely possible I'm doing something stupid in performing all the checks, as far as I can tell, it works for the given case. Because the code itself is not yet very clear and it is not always straightforward what is happening, I'll explain what I have implemented.
First note that for the simplifications that will be made, it is required to have a sum of terms. The first for loop in the method constructs two lists cg_part and other_part, the former consisting of all terms of the sum containing a CG coefficient and the latter the other terms.
Next, we iterate over the list cg_part. The number of CG coefficients is computed, which determines which simplifications can be made (currently, the only implemented simplification uses terms with 1 CG coefficient in each sum term). Those terms with the proper number of CG coefficients are then considered for the simplification. The way this will work is: based on the properties of the CG coefficient in the term, it will search the rest of the list for other terms that can be used in the simplification, and if all the terms exist, will simplify the terms.
Turning to the implementation, when iterating through the list, the first thing to do is determine the properties of the CG coefficient terms, that is to extract from the term in the sum the CG coefficient itself and the numerical leading terms. Here it is also noted the sign of these numerical terms.
Next, the rest of the list is checked to see if a simplification can be made using the determined term. To keep track of this, a list, cg_index, is initialized with False as the element of the list. In checking the later terms, we preform a similar decomposition as with the first term, that is splitting up the CG coefficient from the other components of the term, determining the CG coefficient, the leading terms and the sign of the terms. If the properties of these are correct, then the corresponding element of cg_index is updated with a tuple (term, cg, coeff) where term is the term in cg_part (so this element can be removed later), the CG coefficient and the leading numerical coefficient of the coefficient.
Now, if all the elements of cg_index are changed, the simplification is preformed. When this happens, first we find the minimum coefficient of the chosen CG coefficients, which determines the number of times we can apply the simplification. Then the replacing happens; for each element in cg_index (which is a tuple) the first element of the tuple is popped off cg_part, then, if the term is not eliminated by the simplification, a new term is created and added to cg_part, and finally a constant is added to other_part, completing the simplification.
Looking at the code, this method is very straightforward, but should be robust and scalable for treating cases of sums with numerical leading coefficients, and now that the i's have been dotted and the t's have been crossed on testing this method, implementing new cases should come rapidly in the next couple days. However, one place where this will still need some work is in implementing symbolic simplification, both in dealing with symbolic leading terms on the CG coefficients and symbolic CG coefficients themselves. This will take a bit of thought and likely a bit of help to complete, but this is one thing I hope to work on in the next week. In addition, as the simplification comes into place, I'll work on polishing out the last of the details to get the classes for the Wigner3j/CG coefficients working properly.
First note that for the simplifications that will be made, it is required to have a sum of terms. The first for loop in the method constructs two lists cg_part and other_part, the former consisting of all terms of the sum containing a CG coefficient and the latter the other terms.
Next, we iterate over the list cg_part. The number of CG coefficients is computed, which determines which simplifications can be made (currently, the only implemented simplification uses terms with 1 CG coefficient in each sum term). Those terms with the proper number of CG coefficients are then considered for the simplification. The way this will work is: based on the properties of the CG coefficient in the term, it will search the rest of the list for other terms that can be used in the simplification, and if all the terms exist, will simplify the terms.
Turning to the implementation, when iterating through the list, the first thing to do is determine the properties of the CG coefficient terms, that is to extract from the term in the sum the CG coefficient itself and the numerical leading terms. Here it is also noted the sign of these numerical terms.
Next, the rest of the list is checked to see if a simplification can be made using the determined term. To keep track of this, a list, cg_index, is initialized with False as the element of the list. In checking the later terms, we preform a similar decomposition as with the first term, that is splitting up the CG coefficient from the other components of the term, determining the CG coefficient, the leading terms and the sign of the terms. If the properties of these are correct, then the corresponding element of cg_index is updated with a tuple (term, cg, coeff) where term is the term in cg_part (so this element can be removed later), the CG coefficient and the leading numerical coefficient of the coefficient.
Now, if all the elements of cg_index are changed, the simplification is preformed. When this happens, first we find the minimum coefficient of the chosen CG coefficients, which determines the number of times we can apply the simplification. Then the replacing happens; for each element in cg_index (which is a tuple) the first element of the tuple is popped off cg_part, then, if the term is not eliminated by the simplification, a new term is created and added to cg_part, and finally a constant is added to other_part, completing the simplification.
Looking at the code, this method is very straightforward, but should be robust and scalable for treating cases of sums with numerical leading coefficients, and now that the i's have been dotted and the t's have been crossed on testing this method, implementing new cases should come rapidly in the next couple days. However, one place where this will still need some work is in implementing symbolic simplification, both in dealing with symbolic leading terms on the CG coefficients and symbolic CG coefficients themselves. This will take a bit of thought and likely a bit of help to complete, but this is one thing I hope to work on in the next week. In addition, as the simplification comes into place, I'll work on polishing out the last of the details to get the classes for the Wigner3j/CG coefficients working properly.
Subscribe to:
Posts (Atom)