As expected, my work with Sympy slowed drastically once school started, but nevertheless, I have found enough time to polish off the coupling of arbitrary number of spin spaces that I started over the summer. I'll probably wait until after school is done (and the initial Google Code-In traffic dies down) before opening a pull request, but it has neared the state of conclusion, but I will outline the work done on the branch here.
A notable change from the summer is the coupling and uncoupling code is now much cleaner. The old methods used messy while True: loops which would increment some parameters and check if some end condition was reached, which I found very unsatisfactory and open to some weird use case throwing it into complete disarray. The new methods utilize the notion that any coupling or uncoupling will occur such that there is a well defined change in either the j (in the case of coupling) or m (in the case of uncoupling) values from their maximal values, and this change can be applied over the (un)couplings in the same way you can distribute n balls in m boxes, then it is just matching an integer to a given state and check that the given state is physically feasible.
In addition, I have added all necessary documentation for the new functionality and fixed a few other minor issues with other parts of the new code. I may yet change some of the handling of the j_coupling parameter, but I will reevaluate that when I have more time to look at the code after I finish the semester.
The passing of quantum numbers to define the couplings and un-couplings is still quite verbose, but I see no better way of passing the parameters, hopefully in review someone will see a better way of defining states and couplings.
Sunday, November 27, 2011
Friday, August 19, 2011
Finishing GSoC
So this is the last week of the GSoC program. I'll be writing up a full report on what I've done over the summer here and it will be updated over this next week. This blog post will be recapping this last week of progress and looking forward past the GSoC.
The main thing to report with this last week was the finishing the work on the spin coupling work that was laid out last week and the writing of the code for Coupled spin states, the last pull request I'll get in during the GSoC project is currently open and should only need a last bit of code review to get pulled.
The main thing now is moving beyond the work that will be done during the GSoC project. While I'll be starting classes this next week and I have my qual the next week, so work will definitely slow down. However, this last week, I worked on the multi_coupling branch, which takes the coupling work that is in the current pull and expands it to allow for an arbitrary number of spin bases. The first thing to implement with this was a means of representing the coupling between the spin bases, since the order in which spaces are coupled matters. To do this, I added a jcoupling option to the functions that deal with coupled states. It currently seems pretty messy, but I'm not sure of a better way to do it, as coupling multiple spaces will just pick up a bunch of additional quantum numbers that need to be represented somehow. Basically, this parameter is passed as a list of lists, where each element of the outermost list represents a coupling between two spin spaces. These inner lists have 3 elements, 2 giving the number of the space that is being coupled and the third being the j value of these spaces coupled together. For example, if we wanted to represent a state |j,m,j1,j2,(j12),j3>, the jcoupling would be ( (1,2,j12), ). If this option is not set, then the methods default to coupling the spaces in numerical order, i.e. 1 and 2, then 1,2 and 3, etc. Using this, I have been able to rewrite the uncouple code. The results do not yet have tests, and I'll definitely need to do some calculations by hand to make sure this is working properly, but looking at it, I am pretty confident in the results, tho the code could use some cleaning up.
Moving forward from this would be to get the couple method working with arbitrary spin spaces and run through all of the functions that deal with spin coupling and make sure nothing is still hard coded to use two spin bases. Other than that, the project that I'd set out to work on has been basically completed. I'll continue to work with and develop sympy when I have some spare and hopefully continue to add features and functionality to the quantum module.
The main thing to report with this last week was the finishing the work on the spin coupling work that was laid out last week and the writing of the code for Coupled spin states, the last pull request I'll get in during the GSoC project is currently open and should only need a last bit of code review to get pulled.
The main thing now is moving beyond the work that will be done during the GSoC project. While I'll be starting classes this next week and I have my qual the next week, so work will definitely slow down. However, this last week, I worked on the multi_coupling branch, which takes the coupling work that is in the current pull and expands it to allow for an arbitrary number of spin bases. The first thing to implement with this was a means of representing the coupling between the spin bases, since the order in which spaces are coupled matters. To do this, I added a jcoupling option to the functions that deal with coupled states. It currently seems pretty messy, but I'm not sure of a better way to do it, as coupling multiple spaces will just pick up a bunch of additional quantum numbers that need to be represented somehow. Basically, this parameter is passed as a list of lists, where each element of the outermost list represents a coupling between two spin spaces. These inner lists have 3 elements, 2 giving the number of the space that is being coupled and the third being the j value of these spaces coupled together. For example, if we wanted to represent a state |j,m,j1,j2,(j12),j3>, the jcoupling would be ( (1,2,j12), ). If this option is not set, then the methods default to coupling the spaces in numerical order, i.e. 1 and 2, then 1,2 and 3, etc. Using this, I have been able to rewrite the uncouple code. The results do not yet have tests, and I'll definitely need to do some calculations by hand to make sure this is working properly, but looking at it, I am pretty confident in the results, tho the code could use some cleaning up.
Moving forward from this would be to get the couple method working with arbitrary spin spaces and run through all of the functions that deal with spin coupling and make sure nothing is still hard coded to use two spin bases. Other than that, the project that I'd set out to work on has been basically completed. I'll continue to work with and develop sympy when I have some spare and hopefully continue to add features and functionality to the quantum module.
Friday, August 12, 2011
Getting coupled_spin merged
The biggest development this week was working out what is needed to get the coupled_spin which implements spin coupling merged back into master. There were some things to clean up with non-spin modules and a few minor things to address, but in cleaning this up, there will be some big changes to the way spin coupling works. First, with respect to things that have been implemented, rewrite and represent will no longer handle the coupling and uncoupling of states. To do coupling and uncoupling, instead, a couple and uncouple method will be created to handle the coupling and uncoupling of states. In addition, coupled states will now be represented by new classes, J?KetCoupled for the Cartesian directions. These will be returned by rewrite when a TensorProduct is coupled and will return the proper vector for the coupled space when it is represented and can be uncoupled when an uncoupled operator acts on it.
Most of these new changes have been implemented to varying degrees. There is some functionality lacking, but much of what remains for this is to implement tests for the new functions and make sure everything is working properly.
The coupling of arbitrary number of spin spaces had made slow progress due to some ambiguity when coupled states were created using normal states, but with the new Coupled classes, specifying the coupling should be possible, thus making the computations easier.
Most of these new changes have been implemented to varying degrees. There is some functionality lacking, but much of what remains for this is to implement tests for the new functions and make sure everything is working properly.
The coupling of arbitrary number of spin spaces had made slow progress due to some ambiguity when coupled states were created using normal states, but with the new Coupled classes, specifying the coupling should be possible, thus making the computations easier.
Friday, August 5, 2011
Moving beyond first coupling iteration
In the last week, one of the main things I did was to submit a pull request for the coupled spin machinery that I have been working on. This pull request can be seen here. This implements the coupling and uncoupling operations for states and operators and how these states and operators interact for coupling of two spin states. This pull still has some kinks to work out and some details to iron out, but should be finished up soon.
Moving beyond this pull, the rest of this week has been in working on modifying the coupling methods developed in this pull and making them work for an arbitrary number of spin spaces. The current idea will be to pass a tuple of j values which are to be coupled instead of passing j1 and j2 parameters. While this would work, it would be nice to be able to define how the terms are coupled, noting that the order of how the spaces are coupled matter in determining the coefficients and what will be diagonal in the basis of the coupled states. The current way I am working the coupling is to couple j1 and j2, then couple this to j3, etc. I have currently changed the all the methods to accept the tuple of j values, however, the coupling and uncoupling methods have not been changed to accept arbitrary numbers of spaces. Most of this week has been thinking and trying to determine a good way to implement this machinery that scales to arbitrary numbers of spaces. While it is not directly necessary for dealing with spin states, I will likely also implement Wigner-6j/9j/12j coefficients in cg.py, which will be very similar to the Wigner-3j symbols that were implemented with the Clebsch-Gordan coefficients.
While I am starting to work on this final component of my project, it will be a close call as to whether or not it can get pushed in time to make it in before the end of the project, which will be in just 2 weeks. The initial coupling stuff should get in, but this will be a much closer call. That said, I will definitely see this last part of the project into master.
Moving beyond this pull, the rest of this week has been in working on modifying the coupling methods developed in this pull and making them work for an arbitrary number of spin spaces. The current idea will be to pass a tuple of j values which are to be coupled instead of passing j1 and j2 parameters. While this would work, it would be nice to be able to define how the terms are coupled, noting that the order of how the spaces are coupled matter in determining the coefficients and what will be diagonal in the basis of the coupled states. The current way I am working the coupling is to couple j1 and j2, then couple this to j3, etc. I have currently changed the all the methods to accept the tuple of j values, however, the coupling and uncoupling methods have not been changed to accept arbitrary numbers of spaces. Most of this week has been thinking and trying to determine a good way to implement this machinery that scales to arbitrary numbers of spaces. While it is not directly necessary for dealing with spin states, I will likely also implement Wigner-6j/9j/12j coefficients in cg.py, which will be very similar to the Wigner-3j symbols that were implemented with the Clebsch-Gordan coefficients.
While I am starting to work on this final component of my project, it will be a close call as to whether or not it can get pushed in time to make it in before the end of the project, which will be in just 2 weeks. The initial coupling stuff should get in, but this will be a much closer call. That said, I will definitely see this last part of the project into master.
Saturday, July 30, 2011
Finishing current coupled spin work
This last week I made some good headway towards finishing up the coupled spin state work for the coupling of two spin spaces. The decision was made that spin states should not contain any information as to their coupling, which greatly simplifies not only the code, but also the allowable cases when it comes doing things such as applying operators, rewriting, etc. As such, I am very close to finalizing this stage in the coupled spin work. I will try to fix up the implementation for some symbolic cases that should be doable under the current implementation, but all the current code has tests implemented and docstrings in place, so a pull request will be coming up shortly.
With this stage finishing, I will be moving on to generalizing the current implementation to coupling between more than two spin spaces. I will first need to expand cg.py to include Wigner-6j/9j/etc symbols to describe the coupling between these additional spaces. The logic for spin states will need to be reworked as well, not only to implement these new terms for coupling additional spin spaces, but most of the logic will need to be reworked to allow for an arbitrary number of coupled spin spaces.
While the change to get rid of what would be considered a coupled spin state (that is a state where the state has defined the coupled spaces) does simplify the current implementation, it does limit what can be done. For example, an uncoupled operator could not be applied to a coupled state, as the coupled states would need to be uncoupled, which is only possible if the j values of the coupled states is known. However it was suggested by Brian that a new class be created to deal with coupled states in this sense. Time permitting, I will begin to look at the possibility of implementing such a feature into the current spin framework.
With this stage finishing, I will be moving on to generalizing the current implementation to coupling between more than two spin spaces. I will first need to expand cg.py to include Wigner-6j/9j/etc symbols to describe the coupling between these additional spaces. The logic for spin states will need to be reworked as well, not only to implement these new terms for coupling additional spin spaces, but most of the logic will need to be reworked to allow for an arbitrary number of coupled spin spaces.
While the change to get rid of what would be considered a coupled spin state (that is a state where the state has defined the coupled spaces) does simplify the current implementation, it does limit what can be done. For example, an uncoupled operator could not be applied to a coupled state, as the coupled states would need to be uncoupled, which is only possible if the j values of the coupled states is known. However it was suggested by Brian that a new class be created to deal with coupled states in this sense. Time permitting, I will begin to look at the possibility of implementing such a feature into the current spin framework.
Friday, July 22, 2011
Improving rewrite and represent for coupled/uncoupled states
This last week, most of the coding I have done has been working on getting represent working properly for coupled and uncoupled states. After doing a quick double check on what the basis vectors of a coupled or uncoupled state would be, I was able to get this code in. Tests for the represent logic will still need to be added, but so far it seems to be working properly.
In addition, I modified the rewrite logic to implement the represent method. This way all of the coupling and uncoupling logic is taken care of by represent, just as the represent method also takes care of all rotations of coordinate bases. To simplify the rewrite logic, I also implemented a vect_to_state, which returns a linear combination of states given any state vector when provided with the appropriate parameters, to specify coupled or uncoupled and what the j1 and j2 parameters are.
In addition to this work, I also wrote up the shell of the class that would handle tensor products of operators. However, in its current state, it doesn't function as one would expect, as the _apply_operator_* methods are not being called by qapply. This, in addition to noting that there is very little logic that is in the TensorProductState class has been making me think I can move most of the logic for states and operators that are uncoupled out of the spin class, implementing it instead in places like qapply and represent. The only trick would be the uncoupled-> coupled logic, which is just about the only bit of logic that the TensorProductState class has that couldn't necessarily be generalized, and the loss of the j1/j2/m1/m2 properties. I will be trying to do this in the coming week, which will in turn fix the problems I am having with getting tensor products of states to work.
Saturday, July 16, 2011
Developing coupled/uncoupled states and operators
Most of this last week was spent developing coupled and uncoupled states, beginning to develop how operators will act on these states and writing tests to ensure the code returns the desired result. This week I finished up writing the code for expressing states, and the logic for rewriting from one to the other and back. In addition to this, I implemented the tests which are used for these rewrites. This mostly finishes up the logic for the coupled/uncoupled states, there is still the represent logic which may need to be implemented, tho this will take some looking into to determine what is appropriate and necessary to implement.
For the operators, using the qapply logic already in place, I have begun to implement how operators act on coupled and uncoupled states. I have thus far only implemented logic for coupled operators, that is, for example Jz = Jz_1 + Jz_2(=Jz x 1 + 1 x Jz in an uncoupled representation). In addition to defining how uncoupled product states are acted upon by spin operators, I have expanded those already implemented methods to act on arbitrary states, as they had only previously been defined in how they act on JzKet's. This was done by defining a basis, such that, with the now improved rewrite logic, any state can be rewritten into an appropriate basis for the state and the state in then acted upon by the operator. I have begun to implement the tests that ensure the implemented logic is valid in all cases, both numerical and symbolic, tho this is still a work in progress.
The focus for this next week will be continuing the development of the spin operators, hopefully getting to working with uncoupled spin operators, i.e. operators given in a tensor product to only act on one of the uncoulped states, and developing the tests necessary to the implementation of these states. If I can complete this, I will be closing in on the completion of the coupling of two spin spaces.
Friday, July 8, 2011
Cleaning up simplification and moving into coupled states
So, as I stated in my last post, the first thing I dealt with was fixing up the _cg_simp_add method by implementing pattern matching and move the logic for determining if the simplification can be performed and performing the simplification out of the _cg_simp_add method and developing a system that can easily be expanded to include additional simplifications. To do this, I created another method, _check_cg_simp, which takes various expression to determine if the sum can be simplified. Using Wild variables, the method takes an expression which is matched to the terms of the sum. The method uses a list to store the terms in the sum which can be simplified, so additional expressions are used to determine the length of the list and the index of the items that are matched. There are also additional parameters to handle the leading terms and the sign of the terms. There are still some issues with this method, as when there is more than 1 Clebsch-Gordan coefficient in the sum, then the leading term cannot be matched on the term.
In addition to the finishing of this component of the Clebsch-Gordan coefficient simplification, I have started into working on the coupled spin states and the methods to rewrite them in coupled and uncoupled bases. Coupled spin states are set by passing j1 and j2 parameters when creating the state, for example
>>> JzKet(1,0,j1=1,j2=1)
|1,0,j1=1,j2=1>
These states can be given in the uncoupled basis using the rewrite method and passing coupled=False, so:
>>> JzKet(1,0,j1=1,j2=1).rewrite(Jz, coupled=False)
2**(1/2)*|1,1>x|1,-1>/2-2**(1/2)*|1,-1>x|1,1>/2
This can also be done with a normal state and passing j1 and j2 parameters to the rewrite method, as:
>>> JzKet(1,0).rewrite(Jz, j1=1, j2=1)
2**(1/2)*|1,1>x|1,-1>/2-2**(1/2)*|1,-1>x|1,1>/2
How the coupled states will be handled by rewrite still needs to be addressed, but that will need some thinking and with another GSoC project doing a lot of changes to the represent function, it may take some coordination to get this and the TensorProducts of states and operators working.
Note that in the python expressions above, the states are given as uncoupled states written as tensor products. Uncoupled states will be written as TensorProduct's of states, which will be extended later to spin operators, being written in the uncoupled basis as a TensorProduct. I've just started playing with the uncoupled states and the various methods that will be used to go from uncoupled to coupled states and I've been putting them in a separate TensorProductState class, which subclasses TensorProduct, which keeps all the spin logic separate from the main TensorProduct class, tho this will have to be expanded to include operators. Developing the logic for these uncoupled spin states will be the primary focus of this next week of coding.
Saturday, July 2, 2011
Continuing GSoC work
This last week, I have made progress on my project working on laying the base work for the spin states and in reimplementing logic in the cg_simp method for Clebsch-Gordan coefficients.
First, I have started the work on the implementation of coupled/uncoupled spin states. Currently, this is implemented by adding a coupled property to the spin states. This can be set to True for coupled, False for uncoupled or left as None for other states. As this evolves, I will move to having uncoupled product states be represented by a TensorProduct of two spin states. The next key will be establishing represent and rewrite logic for these spin states. Part of this will be figuring out how exactly these methods will work and what they will return. Namely, the represent method, noting that when representing an uncoupled state as a coupled state, it returns states with multiple j values, which under the current logic, would return matrices of different dimension. Also, we will have to determine what represent will do to uncoupled tensor product spin states. This next week, I will likely rebase this branch against the CG branch so I can start using the Clebsch-Gordan coefficients to implement these functions as the CG pull is finalized.
With the Clebsch-Gordan coefficients, this last week I was able to get the simplification of symbolic Sum objects working. I did this using the pattern matching built into sympy with Wild and .match. The final step with this should be to rework the logic of _cg_simp_add to make it easier to add in additional symmetries.
First, I have started the work on the implementation of coupled/uncoupled spin states. Currently, this is implemented by adding a coupled property to the spin states. This can be set to True for coupled, False for uncoupled or left as None for other states. As this evolves, I will move to having uncoupled product states be represented by a TensorProduct of two spin states. The next key will be establishing represent and rewrite logic for these spin states. Part of this will be figuring out how exactly these methods will work and what they will return. Namely, the represent method, noting that when representing an uncoupled state as a coupled state, it returns states with multiple j values, which under the current logic, would return matrices of different dimension. Also, we will have to determine what represent will do to uncoupled tensor product spin states. This next week, I will likely rebase this branch against the CG branch so I can start using the Clebsch-Gordan coefficients to implement these functions as the CG pull is finalized.
With the Clebsch-Gordan coefficients, this last week I was able to get the simplification of symbolic Sum objects working. I did this using the pattern matching built into sympy with Wild and .match. The final step with this should be to rework the logic of _cg_simp_add to make it easier to add in additional symmetries.
Saturday, June 25, 2011
Transitioning to spin states
This last week, the first thing that was taken care of was finishing the x/y/z spin basis representation. Having fixed the Wigner small d-function in the Rotation class, the tests for this were put into the pull request and the pull was merged into the sympy master, making this my first pull request since starting GSoC. There is still some changes that will come for the Rotation class, namely the creation of a symbolic WignerD class which is returned by the current Rotation.D and Rotation.d functions, but that will be dealt with in a later pull request.
With the x/y/z basis stuff finally out of the way, I moved back to getting the Glebsch-Gordan coefficient/Wigner-3j symbols to a state where they can be pulled. Having fallen behind in getting the CG coefficient simplification to a suitable state and with the work on the x/y/z spin basis pushing the timeline back even further, the current goal is to merge what I have so far and move on to the coupled spin states. What I have so far is the classes for the Wigner-3j symbols and the Clebsch-Gordan coefficients which can be manipulated symbolically and evaluated, and a very rough version of the cg_simp method. Currently, this method can handle 3 numerical simplification, however the code is still messy and having more cases would be ideal. That said, in an effort to make sure the key parts of this GSoC project are covered, I'll be moving into writing the coupled spin states.
For the spin states portion of this project, I will develop a means of writing coupled and uncoupled spin states. The uncoupled product basis states will be written using the TensorProduct, which is in the current quantum module; each of the states in the tensor product will be states as they are currently implemented. To represent coupled basis spin states, the current spin states will be modified to included a coupled parameter. This value stores the J_i's of the spin spaces which are being coupled. In addition to the spin states being implemented, methods will be written to utilize the CG coefficients mentioned earlier to go between coupled and uncoupled basis representation. Look for more next week as this code is fleshed out.
With the x/y/z basis stuff finally out of the way, I moved back to getting the Glebsch-Gordan coefficient/Wigner-3j symbols to a state where they can be pulled. Having fallen behind in getting the CG coefficient simplification to a suitable state and with the work on the x/y/z spin basis pushing the timeline back even further, the current goal is to merge what I have so far and move on to the coupled spin states. What I have so far is the classes for the Wigner-3j symbols and the Clebsch-Gordan coefficients which can be manipulated symbolically and evaluated, and a very rough version of the cg_simp method. Currently, this method can handle 3 numerical simplification, however the code is still messy and having more cases would be ideal. That said, in an effort to make sure the key parts of this GSoC project are covered, I'll be moving into writing the coupled spin states.
For the spin states portion of this project, I will develop a means of writing coupled and uncoupled spin states. The uncoupled product basis states will be written using the TensorProduct, which is in the current quantum module; each of the states in the tensor product will be states as they are currently implemented. To represent coupled basis spin states, the current spin states will be modified to included a coupled parameter. This value stores the J_i's of the spin spaces which are being coupled. In addition to the spin states being implemented, methods will be written to utilize the CG coefficients mentioned earlier to go between coupled and uncoupled basis representation. Look for more next week as this code is fleshed out.
Saturday, June 18, 2011
More CG simplification and wrapping up x/y/z spin bases
For the first part of this last week, I continued on my work to get sums of Clebsch-Gordan coefficients to simplify. Using the same general logic that I outlined in the last blog entry, besides general cleaning up of the code, most of the work at the beginning of the week was spent on trying to develop a function that could check an expression for CG coefficients matching a set of conditions.
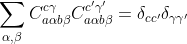
While the current method would be able to check for specific values on the CG coefficients, I have yet to come up with a good way to check that the m1 and m2 values are the same when they can take any value, as in this example. As it stands, this code still seems like quite a hack and will need some work before it is good to go.
What is left with this part of the project is:
- Getting simplification to work with sums of products of terms (as in the example above)
- Applying CG symmetries to perform simplifications
- Simplification of symbolic CG sums
- Fixing up the printing of CG terms
- Final testing/documentation
This part of the project has unfortunately fallen behind the preliminary schedule by a bit, as it was due to be finished up last week. I'll outline what I'm currently working on finish up next, but hopefully I can finish the CG stuff ASAP so I can move on to working on the spin stuff which is the true meat of the project and try to get back on schedule.
The rationale behind trying to write such a method is that it would make it much easier to identify the times where symmetries could be utilized. With such a method, the process of checking for CG coefficients could be done in a single function and the logic for implementing CG symmetries could be handled in this one function. The current method uses lists of tuples to specify the conditions on CG coefficients. For example, if the j1 value of a CG coefficient needed to be =0, you could pass the tuple ("j1",0), or if the m1 and m3 values match ("m1","m3"). All the conditions for each CG coefficient are combined into a single tuple. The current snag with simplifications of sums of products of CG coefficients. For example:
While the current method would be able to check for specific values on the CG coefficients, I have yet to come up with a good way to check that the m1 and m2 values are the same when they can take any value, as in this example. As it stands, this code still seems like quite a hack and will need some work before it is good to go.
What is left with this part of the project is:
- Getting simplification to work with sums of products of terms (as in the example above)
- Applying CG symmetries to perform simplifications
- Simplification of symbolic CG sums
- Fixing up the printing of CG terms
- Final testing/documentation
This part of the project has unfortunately fallen behind the preliminary schedule by a bit, as it was due to be finished up last week. I'll outline what I'm currently working on finish up next, but hopefully I can finish the CG stuff ASAP so I can move on to working on the spin stuff which is the true meat of the project and try to get back on schedule.
After meeting with my project mentor, Ondrej, on Wednesday, it was decided that the focus would shift to finishing up the work I'd started on x/y/z spin bases and representation of spin states that I'd started before GSoC had officially started.
The first order of business was identifying an error in the Wigner small-d function, which is used extensively in the changing of spin bases. With Ondrej noting that the small-d function was defined only on a small interval and then me discovering the bug in the Rotation.d method, we were able to address this. However, no sooner had this been done than Ondrej is able to work out a better equation for the small-d function, which will likely replace the current implementation.
Other than this, most of the work this week on the x/y/z basis representation was in documentation, testing and generally cleaning up the code to be pulled. The current pull request (my first work to be submitted since the start of GSoC) is still open here. While this pull integrates the current work on basis representation, after this pull there is still some work that will need to be done testing both the Wigner small-d and the D functions, for both symbolic and numerical values, and ensuring they return the correct results. Because the representation code relies so heavily on these functions, it is imperative that these functions evaluate properly. Once these are fully tested, there will also likely need to be more tests to ensure all the representation code returns the right values for as many odd cases as would be necessary to test. Hopefully I can finish this up soon and move on to other work that still needs to be done.
Saturday, June 11, 2011
More improvements to the simplification method
I was out of town for the beginning of this week, so I don't have as much to report, nevertheless in the last few days, I have made some good improvements to the cg_simp method, allowing it to simplify cases other than just the simple sums, tho it still only handles the same case as before involving the sum of . While it is entirely possible I'm doing something stupid in performing all the checks, as far as I can tell, it works for the given case. Because the code itself is not yet very clear and it is not always straightforward what is happening, I'll explain what I have implemented.
First note that for the simplifications that will be made, it is required to have a sum of terms. The first for loop in the method constructs two lists cg_part and other_part, the former consisting of all terms of the sum containing a CG coefficient and the latter the other terms.
Next, we iterate over the list cg_part. The number of CG coefficients is computed, which determines which simplifications can be made (currently, the only implemented simplification uses terms with 1 CG coefficient in each sum term). Those terms with the proper number of CG coefficients are then considered for the simplification. The way this will work is: based on the properties of the CG coefficient in the term, it will search the rest of the list for other terms that can be used in the simplification, and if all the terms exist, will simplify the terms.
Turning to the implementation, when iterating through the list, the first thing to do is determine the properties of the CG coefficient terms, that is to extract from the term in the sum the CG coefficient itself and the numerical leading terms. Here it is also noted the sign of these numerical terms.
Next, the rest of the list is checked to see if a simplification can be made using the determined term. To keep track of this, a list, cg_index, is initialized with False as the element of the list. In checking the later terms, we preform a similar decomposition as with the first term, that is splitting up the CG coefficient from the other components of the term, determining the CG coefficient, the leading terms and the sign of the terms. If the properties of these are correct, then the corresponding element of cg_index is updated with a tuple (term, cg, coeff) where term is the term in cg_part (so this element can be removed later), the CG coefficient and the leading numerical coefficient of the coefficient.
Now, if all the elements of cg_index are changed, the simplification is preformed. When this happens, first we find the minimum coefficient of the chosen CG coefficients, which determines the number of times we can apply the simplification. Then the replacing happens; for each element in cg_index (which is a tuple) the first element of the tuple is popped off cg_part, then, if the term is not eliminated by the simplification, a new term is created and added to cg_part, and finally a constant is added to other_part, completing the simplification.
Looking at the code, this method is very straightforward, but should be robust and scalable for treating cases of sums with numerical leading coefficients, and now that the i's have been dotted and the t's have been crossed on testing this method, implementing new cases should come rapidly in the next couple days. However, one place where this will still need some work is in implementing symbolic simplification, both in dealing with symbolic leading terms on the CG coefficients and symbolic CG coefficients themselves. This will take a bit of thought and likely a bit of help to complete, but this is one thing I hope to work on in the next week. In addition, as the simplification comes into place, I'll work on polishing out the last of the details to get the classes for the Wigner3j/CG coefficients working properly.
First note that for the simplifications that will be made, it is required to have a sum of terms. The first for loop in the method constructs two lists cg_part and other_part, the former consisting of all terms of the sum containing a CG coefficient and the latter the other terms.
Next, we iterate over the list cg_part. The number of CG coefficients is computed, which determines which simplifications can be made (currently, the only implemented simplification uses terms with 1 CG coefficient in each sum term). Those terms with the proper number of CG coefficients are then considered for the simplification. The way this will work is: based on the properties of the CG coefficient in the term, it will search the rest of the list for other terms that can be used in the simplification, and if all the terms exist, will simplify the terms.
Turning to the implementation, when iterating through the list, the first thing to do is determine the properties of the CG coefficient terms, that is to extract from the term in the sum the CG coefficient itself and the numerical leading terms. Here it is also noted the sign of these numerical terms.
Next, the rest of the list is checked to see if a simplification can be made using the determined term. To keep track of this, a list, cg_index, is initialized with False as the element of the list. In checking the later terms, we preform a similar decomposition as with the first term, that is splitting up the CG coefficient from the other components of the term, determining the CG coefficient, the leading terms and the sign of the terms. If the properties of these are correct, then the corresponding element of cg_index is updated with a tuple (term, cg, coeff) where term is the term in cg_part (so this element can be removed later), the CG coefficient and the leading numerical coefficient of the coefficient.
Now, if all the elements of cg_index are changed, the simplification is preformed. When this happens, first we find the minimum coefficient of the chosen CG coefficients, which determines the number of times we can apply the simplification. Then the replacing happens; for each element in cg_index (which is a tuple) the first element of the tuple is popped off cg_part, then, if the term is not eliminated by the simplification, a new term is created and added to cg_part, and finally a constant is added to other_part, completing the simplification.
Looking at the code, this method is very straightforward, but should be robust and scalable for treating cases of sums with numerical leading coefficients, and now that the i's have been dotted and the t's have been crossed on testing this method, implementing new cases should come rapidly in the next couple days. However, one place where this will still need some work is in implementing symbolic simplification, both in dealing with symbolic leading terms on the CG coefficients and symbolic CG coefficients themselves. This will take a bit of thought and likely a bit of help to complete, but this is one thing I hope to work on in the next week. In addition, as the simplification comes into place, I'll work on polishing out the last of the details to get the classes for the Wigner3j/CG coefficients working properly.
Tuesday, May 31, 2011
Implementing Clebsch-Gordan symmetries and sum properties
In this first week of the GSoC project, I focused on implementing methods that would simplify terms with Clebsch-Gordan coefficients. This still has a long was to go, but I will outline what I have done so far.
The first step was implementing means of dealing with sums of single coefficients. This would hopefully look something like:
>>>Sum(CG(a,alpha,0,0,a,alpha),(alpha,-a,a+1))
2*a+1
The first implementation of this used an indexing system that was able to index single coefficients, which could then be processed. This allowed the simplification function to act properly in simple numerical cases, so it could do things like:
>>>cg_simp(CG(1,-1,0,0,1,-1)+CG(1,0,0,0,1,0)+CG(1,1,0,0,1,1)+a)
a+3
The problem with this implementation is doing something as simple as having one of the terms have a constant coefficient would break it. In addition, there would be no clear way to extend this to sums involving products of multiple Clebsch-Gordan coefficients.
To deal with this, I started working a solution that could deal with having constant coefficients and products of coefficients. Currently implemented is method which creates list of tuples containing information about the Clebsch-Gordan coefficients and the leading coefficients of the Clebsch-Gordan coefficients. Currently, the only implemented logic is only able to deal with the case in that could be dealt with in the previous implementation, however, this should be able to expand to encompass more exotic cases.
Another thing that was touched on this last week was treating symmetries. These are quite simple to implement, as they need only return new Clebsch-Gordan coefficients in place of old ones, just with the parameters changed in correspondence with the symmetry operation. The key will be using these symmetries to help in simplifying terms. This will be based on the development of better logic in the simplification method and the implementation of some means of determining if these symmetries can be used to apply some property of the Clebsch-Gordan coefficients that can simplify the expression.
I will be out of town this next week on a vacation, and will not be able to get work in, but I will continue working on this when I return, with the intention of getting it to a state that can be pushed within the next couple weeks.
The first step was implementing means of dealing with sums of single coefficients. This would hopefully look something like:
>>>Sum(CG(a,alpha,0,0,a,alpha),(alpha,-a,a+1))
2*a+1
The first implementation of this used an indexing system that was able to index single coefficients, which could then be processed. This allowed the simplification function to act properly in simple numerical cases, so it could do things like:
>>>cg_simp(CG(1,-1,0,0,1,-1)+CG(1,0,0,0,1,0)+CG(1,1,0,0,1,1)+a)
a+3
The problem with this implementation is doing something as simple as having one of the terms have a constant coefficient would break it. In addition, there would be no clear way to extend this to sums involving products of multiple Clebsch-Gordan coefficients.
To deal with this, I started working a solution that could deal with having constant coefficients and products of coefficients. Currently implemented is method which creates list of tuples containing information about the Clebsch-Gordan coefficients and the leading coefficients of the Clebsch-Gordan coefficients. Currently, the only implemented logic is only able to deal with the case in that could be dealt with in the previous implementation, however, this should be able to expand to encompass more exotic cases.
Another thing that was touched on this last week was treating symmetries. These are quite simple to implement, as they need only return new Clebsch-Gordan coefficients in place of old ones, just with the parameters changed in correspondence with the symmetry operation. The key will be using these symmetries to help in simplifying terms. This will be based on the development of better logic in the simplification method and the implementation of some means of determining if these symmetries can be used to apply some property of the Clebsch-Gordan coefficients that can simplify the expression.
I will be out of town this next week on a vacation, and will not be able to get work in, but I will continue working on this when I return, with the intention of getting it to a state that can be pushed within the next couple weeks.
Tuesday, May 24, 2011
Official GSoC start
This week marks the official start of the Google Summer of Code. While I started getting my feet wet last week after finishing the last of my finals and grading, the bulk of the work has just started turning out. I'll quick cover what I have from this last week and what I'm looking to get working this week.
Before the start, I worked out expanding the functionality of the currently implemented x/y/z bases, which work I have here. The previous implementation only allowed for evaluating inner products between states in the same basis and representing the states in the Jz basis and then only with j=1/2 states. Using the Wigner D-function, implemented with the Rotation class, I implemented represent to go between the x/y/z bases for any j values. Both _eval_innerproduct and _rewrite_as were then created to take advantage of the represent function to extend the functionality of the inner product and to implement rewrite between any bases and any arbitrary j values.
This seems like this is some documentation and tests away from being pushed, but there is something buggy with the Rotation.d function, implementing the Wigner small d-matrix. I noticed when trying to do
>>>qapply(JzBra(1,1)*JzKet(1,1).rewrite('Jx')
and I wasn't getting the right answer. As it turns out, the Rotation.d function, which uses Varshalovich 4.3.2 Eq 7, does not give the right answer for Rotation.d(1,1,0,-pi/2) or Rotation.d(1,0,1,pi/2). Namely, there is something wrong with the equation that doesn't change the sign of the matrix element when reversing the sign of the beta Euler angle. Running all four differential representations given by Varshalovich for the small d matrix, Eq 7-10, give the wrong result, so the derivations of these will need to be checked to fix this. I have a bug report up here.
As for what I will be implementing this week, I already have the basics of the Wigner3j and CG class implemented, the work for this going up here. This includes creating the objects, _some_ of the printing functionality and numerical evaluation of the elements using the wigner.py functions. The meat of the class that I'm currently working on is the cg_simp function, which will simplify expressions of Clebsch-Gordan coefficients. I currently have one case working, that is
Sum(CG(a,alpha,0,0,a,alpha),(alpha,-a,a)) == 2a+1
which is Varshalovich 8.7.1 Eq 1. There are still some things to smooth out with the implementation, but I should have that worked out a bit better, in addition to some more simplifications by the end of the week.
That's all I have for now, watch for updates within the week as to what I've gotten done and what I have yet to do.
Before the start, I worked out expanding the functionality of the currently implemented x/y/z bases, which work I have here. The previous implementation only allowed for evaluating inner products between states in the same basis and representing the states in the Jz basis and then only with j=1/2 states. Using the Wigner D-function, implemented with the Rotation class, I implemented represent to go between the x/y/z bases for any j values. Both _eval_innerproduct and _rewrite_as were then created to take advantage of the represent function to extend the functionality of the inner product and to implement rewrite between any bases and any arbitrary j values.
This seems like this is some documentation and tests away from being pushed, but there is something buggy with the Rotation.d function, implementing the Wigner small d-matrix. I noticed when trying to do
>>>qapply(JzBra(1,1)*JzKet(1,1).rewrite('Jx')
and I wasn't getting the right answer. As it turns out, the Rotation.d function, which uses Varshalovich 4.3.2 Eq 7, does not give the right answer for Rotation.d(1,1,0,-pi/2) or Rotation.d(1,0,1,pi/2). Namely, there is something wrong with the equation that doesn't change the sign of the matrix element when reversing the sign of the beta Euler angle. Running all four differential representations given by Varshalovich for the small d matrix, Eq 7-10, give the wrong result, so the derivations of these will need to be checked to fix this. I have a bug report up here.
As for what I will be implementing this week, I already have the basics of the Wigner3j and CG class implemented, the work for this going up here. This includes creating the objects, _some_ of the printing functionality and numerical evaluation of the elements using the wigner.py functions. The meat of the class that I'm currently working on is the cg_simp function, which will simplify expressions of Clebsch-Gordan coefficients. I currently have one case working, that is
Sum(CG(a,alpha,0,0,a,alpha),(alpha,-a,a)) == 2a+1
which is Varshalovich 8.7.1 Eq 1. There are still some things to smooth out with the implementation, but I should have that worked out a bit better, in addition to some more simplifications by the end of the week.
That's all I have for now, watch for updates within the week as to what I've gotten done and what I have yet to do.
Monday, April 25, 2011
The best things in life are free (and open source)
Hi all,
This adventure into blogging is to document the work I will be doing this summer with SymPy, an open source symbolic mathematics library written in Python. The project will be done as a part of the Google Summer of Code program. This summer, I will be developing a symbolic class for creating Clebsch-Gordan coefficients and will develop the spin algebra in the existing quantum physics module to utilize these coefficients. The gory details can be read in my application. My mentor for this project will be Ondřej Čertík. The project officially starts May 24, but I'll be diving in once I finish up the last of my finals May 14. I will be documenting my progress on the project throughout the summer through this blog, and anyone interested in this is free to watch for updates once the project is underway. All my work will be pushed to my SymPy fork on github.
That's enough for now, I'll be checking back in once I get started in the summer. Now, back to trying to graduate.
This adventure into blogging is to document the work I will be doing this summer with SymPy, an open source symbolic mathematics library written in Python. The project will be done as a part of the Google Summer of Code program. This summer, I will be developing a symbolic class for creating Clebsch-Gordan coefficients and will develop the spin algebra in the existing quantum physics module to utilize these coefficients. The gory details can be read in my application. My mentor for this project will be Ondřej Čertík. The project officially starts May 24, but I'll be diving in once I finish up the last of my finals May 14. I will be documenting my progress on the project throughout the summer through this blog, and anyone interested in this is free to watch for updates once the project is underway. All my work will be pushed to my SymPy fork on github.
That's enough for now, I'll be checking back in once I get started in the summer. Now, back to trying to graduate.
Subscribe to:
Posts (Atom)